三種類の二元数(二重数、複素数、分解型複素数)を行列で表現します。
『行列と代数系』シリーズの記事です。
- 実二次正方行列の初歩
- 実二次正方行列と代数系
- 冪零行列と二重数
- 三種類の二元数 ← この記事
- 分解型四元数と同型対応
- 分解型四元数と幾何代数
- 行列表現と外積と行列式
- 分解型複素数と固有値
目次
二重数
前々回、二重数を導入して行列で表現しました。
\textcolor{red}{a}+\textcolor{red}{b}ε
~↦~
a\underbrace{\begin{pmatrix}1&0\\0&1\end{pmatrix}}_1
+b\underbrace{\begin{pmatrix}0&0\\1&0\end{pmatrix}}_ε
=\underbrace{\begin{pmatrix}\textcolor{red}{a}&0\\\textcolor{red}{b}&a\end{pmatrix}}_{a+bε}
赤字になっているのは、表現行列の左半分を見れば $a+bε$ の係数との対応が分かりやすいことを示します。
表現行列の右上の $0$ は $ε²=0$ に対応します。これは次のように確認できます。
\begin{pmatrix}0&x\\1&0\end{pmatrix}^2=xI
行列を2乗すると右上の成分が単位行列の係数として表れます。
右上の成分(2乗したときの値)を変更すれば、虚数 $i ^ 2=-1$ も行列で表現できます。
\textcolor{red}{a}+\textcolor{red}{b}i
~↦~
a\underbrace{\begin{pmatrix}1&0\\0&1\end{pmatrix}}_1
+b\underbrace{\begin{pmatrix}0&-1\\1&0\end{pmatrix}}_i
=\underbrace{\begin{pmatrix}\textcolor{red}{a}&-b\\\textcolor{red}{b}&a\end{pmatrix}}_{a+bi}
※ 表現行列には $a$ と $b$ が2回現れて冗長ですが、これについては後述します。
複素数の計算と行列の計算が対応します。
\begin{aligned}
(\textcolor{red}{a}+\textcolor{red}{b}i)
(\textcolor{red}{c}+\textcolor{red}{d}i)
&=(\textcolor{red}{ac-bd})+(\textcolor{red}{ad+bc})i
\\
\begin{pmatrix}\textcolor{red}{a}&-b\\\textcolor{red}{b}&a\end{pmatrix}
\begin{pmatrix}\textcolor{red}{c}&-d\\\textcolor{red}{d}&c\end{pmatrix}
&=\begin{pmatrix}\textcolor{red}{ac-bd}&-(ad+bc)\\\textcolor{red}{ad+bc}&ac-bd\end{pmatrix}
\end{aligned}
複素数の積は交換しますが、表現行列の積も交換します。
\begin{aligned}
(\textcolor{red}{c}+\textcolor{red}{d}i)
(\textcolor{red}{a}+\textcolor{red}{b}i)
&=(\textcolor{red}{ac-bd})+(\textcolor{red}{ad+bc})i
\\
\begin{pmatrix}\textcolor{red}{c}&-d\\\textcolor{red}{d}&c\end{pmatrix}
\begin{pmatrix}\textcolor{red}{a}&-b\\\textcolor{red}{b}&a\end{pmatrix}
&=\begin{pmatrix}\textcolor{red}{ac-bd}&-(ad+bc)\\\textcolor{red}{ad+bc}&ac-bd\end{pmatrix}
\end{aligned}
計算過程を見ると、表現行列の冗長性が交換に必要なことが伺えます。同じ行列が積の左に来た時と右に来た時では計算に使われる成分の順序が異なりますが、同じ情報を複数持っていることでうまく整合しています。
また、冗長性により表現行列の計算は複素数の計算に比べて無駄(オーバーヘッド)があります。ですが、行列表現は計算の効率化よりも複素数を調べる手段として行列が使えることにメリットがあります。
表現行列の形から零行列となる $a=b=0$ 以外は正則であることが分かります。
\begin{pmatrix}a&-b\\b&a\end{pmatrix}
\quad a^2+b^2≠0\quad(a≠0,b≠0)
複素数の逆数と表現行列の逆行列が対応します。
(a+bi)^{-1}
=\frac1{a+bi}
=\frac{a-bi}{(a+bi)(a-bi)}
=\frac{a-bi}{a^2+b^2}
\begin{pmatrix}a&-b\\b&a\end{pmatrix}^{-1}
=\frac1{a^2+b^2}
\underbrace{\begin{pmatrix}a&b\\-b&a\end{pmatrix}}_{a-bi}
二重数では行列と一次変数変換との対応にあまり意味がないと書きましたが、複素数では大いに意味があります。
行列と一次変数変換を対応させることで複素平面がつながります。
\begin{cases}
x=ax'-by' \\
y=bx'+ay'
\end{cases}
\quad
\begin{pmatrix}a&-b\\b&a\end{pmatrix}
\quad
a+bi
$(x',y')=(1,0)$ を代入して得られる $(x,y)=(a,b)$ が複素平面上の点に対応します。考え方としては $(1,0)$ を $a+bi$ によって変換した点が $(a,b)$ となります。

複素数の積によって変換が合成される様子が伺えます。
\begin{aligned}
&\begin{cases}
x'=cx''-dy'' \\
y'=dx''+cy''
\end{cases}
\quad
\begin{pmatrix}c&-d\\d&c\end{pmatrix}
\quad
c+di
\\
&\begin{cases}
x=a(cx''-dy'')-b(dx''+cy'')=(ac-bd)x''-(ad+bc)y'' \\
y=b(cx''-dy'')+a(dx''+cy'')=(ad+bc)x''+(ac-bd)y''
\end{cases}
\end{aligned}
\begin{aligned}
\begin{pmatrix}a&-b\\b&a\end{pmatrix}
\begin{pmatrix}c&-d\\d&c\end{pmatrix}
&=\begin{pmatrix}ac-bd&-(ad+bc)\\ad+bc&ac-bd\end{pmatrix}
\\
(a+bi)(c+di)&=(ac-bd)+(ad+bc)i
\end{aligned}
今回は複素平面についての説明が目的ではないためこの辺で切り上げます。いずれ機会を改めて取り上げる予定です。
虚数単位を2乗した値が、複素数は $-1$、二重数は $0$ でした。それでは $1$ もあるのではないかと考えるのが自然な成り行きです。これは分解型複素数と呼ばれます。
分解型複素数の虚数単位は $j$ と表記して $j ^ 2=1$ です。$j=1$ または $-1$ ではないかと混乱を招きがちですが、行列表現によって $±1$ と $j$ とは別物だとはっきりします。
\textcolor{red}{a}+\textcolor{red}{b}j
~↦~
a\underbrace{\begin{pmatrix}1&0\\0&1\end{pmatrix}}_1
+b\underbrace{\begin{pmatrix}0&1\\1&0\end{pmatrix}}_j
=\underbrace{\begin{pmatrix}\textcolor{red}{a}&b\\\textcolor{red}{b}&a\end{pmatrix}}_{a+bj}
分解型複素数の積も交換します。
\begin{aligned}
(\textcolor{red}{a}+\textcolor{red}{b}j)
(\textcolor{red}{c}+\textcolor{red}{d}j)
&=(\textcolor{red}{ac+bd})+(\textcolor{red}{ad+bc})j
\\
\begin{pmatrix}\textcolor{red}{a}&b\\\textcolor{red}{b}&a\end{pmatrix}
\begin{pmatrix}\textcolor{red}{c}&d\\\textcolor{red}{d}&c\end{pmatrix}
&=\begin{pmatrix}\textcolor{red}{ac+bd}&ad+bc\\\textcolor{red}{ad+bc}&ac+bd\end{pmatrix}
\end{aligned}
\begin{aligned}
(\textcolor{red}{c}+\textcolor{red}{d}j)
(\textcolor{red}{a}+\textcolor{red}{b}j)
&=(\textcolor{red}{ac+bd})+(\textcolor{red}{ad+bc})j
\\
\begin{pmatrix}\textcolor{red}{c}&d\\\textcolor{red}{d}&c\end{pmatrix}
\begin{pmatrix}\textcolor{red}{a}&b\\\textcolor{red}{b}&a\end{pmatrix}
&=\begin{pmatrix}\textcolor{red}{ac+bd}&ad+bc\\\textcolor{red}{ad+bc}&ac+bd\end{pmatrix}
\end{aligned}
分解型複素数の表現行列はマイナスが表れないためすっきりした形をしていますが、複素数とは異なり正則となる表現行列に制限があります。
$a ^ 2≠b ^ 2$ となる場合、分解型複素数には逆数が存在して、表現行列にも逆行列が存在します。
(a+bj)^{-1}
=\frac1{a+bj}
=\frac{a-bj}{(a+bj)(a-bj)}
=\frac{a-bj}{a^2-b^2}
\begin{pmatrix}a&b\\b&a\end{pmatrix}^{-1}
=\frac1{a^2-b^2}
\underbrace{\begin{pmatrix}a&-b\\-b&a\end{pmatrix}}_{a-bj}
逆数の分母に現れる $a ^ 2-b ^ 2$ は符号が $+,-$ となっています。このように符号が同数に分かれることを分解型符号数と呼んで、分解型複素数の名前の由来となっています。
$a ^ 2=b ^ 2$ となる場合、表現行列は非正則です。これは分解型複素数に零因子が存在することを意味します。例を示します。
(1+j)(1-j)=1-1=0
\begin{pmatrix}1&1\\1&1\end{pmatrix}
\begin{pmatrix}1&-1\\-1&1\end{pmatrix}
=\begin{pmatrix}1-1&-1+1\\1-1&-1+1\end{pmatrix}=O
※ これを説明するため前回は零因子を取り上げました。
分解型複素数でも分解型複素平面を考えることは可能です。非正則な値に対応する点は原点を中心に X 字形をしています。
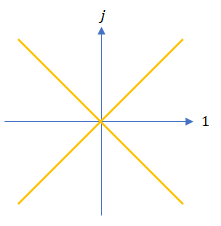
※ この X 字形は特殊相対性理論で光円錐と呼ばれます。分解型複素数を特殊相対性理論の計算に応用することも可能です。いずれ機会を改めて取り上げる予定です。
直和分解
先ほど $a ^ 2 - b ^ 2$ の符号が分かれることが分解の由来だと書きましたが、それ以外にも分解の性質を持っています。
非正則な例で取り上げた $1+j$ を2乗すると、2倍になります。
(1+j)^2=1+2j+1=2(1+j)
※ 非正則行列をケイリー・ハミルトンの定理で2乗したのと同じ振る舞いです。
半分にして2乗すると、元の値のままです。このような性質を冪等と呼びます。
\left(\frac{1+j}2\right)^2
=\frac{2(1+j)}4
=\frac{1+j}2
同様に次も冪等です。
\left(\frac{1-j}2\right)^2
=\frac{2(1-j)}4
=\frac{1-j}2
これらをそれぞれ $i',j'$ と置いて、和と差と積を確認します。零因子です。
i'=\frac{1+j}2,\ j'=\frac{1-j}2
i'+j'=1,\ i'-j'=j,\ i'j'=j'i'=0
任意の分解型複素数を $i',j'$ に係数を付けて表すことが可能です。$1,j$ や $i',j'$ のように組み合わせて単位として扱える元を基底と呼びます。
a+bj=a(i'+j')+b(i'-j')=(a+b)i'+(a-b)j'
※ 光円錐上の零因子となる冪等元から基底を取ったということです。

$i',j'$ で表記した分解型複素数の積を計算します。
(ai'+bj')(ci'+dj')=aci'+bdj'
零因子であることからクロスターム $i'j'$ が消えて、同じ基底の係数を掛けたものだけが残りました。これは2つの掛け算を独立に行ったと解釈できます。
分解型複素数は基底を変えて見れば2つの実数に分解されて、積は個々に計算されるということです。この種の分解を直和分解と呼びます。直和の記号 $⊕$ で表記すれば次の通りです。
(a⊕b)(c⊕d)=ac⊕bd
これは2つの数をセットにして扱うという考え方です。同じことを順序対(タプル)で表記すれば次の通りです。
(a,b)(c,d)=(ac,bd)
以下を参考にしました。
Exchange matrix
$j$ の表現行列を一次変数変換に対応させると、$x$ と $y$ を入れ替えることが分かります。
\begin{cases}
x=y' \\
y=x'
\end{cases}
\quad
\begin{pmatrix}0&1\\1&0\end{pmatrix}
\quad
j
入れ替えを2回行うと元に戻ることから $j ^ 2=1$ が理解できます。
この種の行列を英語では exchange matrix と呼ぶようですが、日本語で交換行列と呼ぶのは見たことがないため、訳さずにおきました。
三種類の二元数
複素数、分解型複素数、二重数をまとめて三種類の二元数と呼びます。
同型を除いて、実数体上二次元の単位的多元環は通常の複素数体、分解型複素数環、二重数環のちょうど三種類しかない。
各 2×2 実行列は三種類の一般化された複素数(つまり、通常の複素数、二重数、分解型複素数)のひとつとして解釈できる。
まとめとして、これら三種類の二元数の表現行列を再掲します。
\begin{aligned}
\textcolor{red}{a}+\textcolor{red}{b}i
&~↦~
a\underbrace{\begin{pmatrix}1&0\\0&1\end{pmatrix}}_1
+b\underbrace{\begin{pmatrix}0&-1\\1&0\end{pmatrix}}_i
=\underbrace{\begin{pmatrix}\textcolor{red}{a}&-b\\\textcolor{red}{b}&a\end{pmatrix}}_{a+bi}
\\
\textcolor{red}{a}+\textcolor{red}{b}j
&~↦~
a\underbrace{\begin{pmatrix}1&0\\0&1\end{pmatrix}}_1
+b\underbrace{\begin{pmatrix}0&1\\1&0\end{pmatrix}}_j
=\underbrace{\begin{pmatrix}\textcolor{red}{a}&b\\\textcolor{red}{b}&a\end{pmatrix}}_{a+bj}
\\
\textcolor{red}{a}+\textcolor{red}{b}ε
&~↦~
a\underbrace{\begin{pmatrix}1&0\\0&1\end{pmatrix}}_1
+b\underbrace{\begin{pmatrix}0&0\\1&0\end{pmatrix}}_ε
=\underbrace{\begin{pmatrix}\textcolor{red}{a}&0\\\textcolor{red}{b}&a\end{pmatrix}}_{a+bε}
\end{aligned}
虚数単位の右上の成分が2乗したときの値に対応します。
\begin{pmatrix}0&x\\1&0\end{pmatrix}^2=xI
adhara_mathphysさんのツイートで三種類の二元数という分類を知りました。
三種類の二元数についてオイラーの公式を考える記事です。
分解型複素数のオイラーの公式は特殊相対性理論を考える上でも役に立ちます。
◀前の記事 ▲記事一覧 次の記事▶


