ディラック作用素を計算して、2次元や4次元のベクトル解析を調べます。
【2018.07.25】全面的に改訂しました。
シリーズの記事です。
- ディラック作用素と外微分・余微分
- ディラック作用素とラプラシアン
- ディラック作用素で2次元と4次元を計算 ← この記事
計算には以下で作成したプログラムを使用します。
マクスウェル方程式や複素解析への応用は以下の記事を参照してください。
微分形式の余微分は以下の記事を参照してください。
目次
ディラック作用素はスカラー値関数 $f$ の全微分 $Df$ と基底とを、クリフォード代数の幾何積で計算します。基底を $ξ$ とすれば:
D(fξ)=(Df)ξ
ディラック作用素の計算結果にはグレードが上がる部分と下がる部分があります。グレードが上がる部分は外微分 $d$、グレードが下がる部分は余微分 $δ$ の符号反転と一致します。
D=d-δ
次元が空間基底だけで構成されています。
3次元
ベクトル解析ではスカラー場の微分をgrad、ベクトル場の微分をrot/divと呼びます。
\begin{aligned}
\mathrm{grad}\,F&=\left(\begin{matrix}F_x\\F_y\\F_z\end{matrix}\right)\\
\mathrm{rot}\left(\begin{matrix}X\\Y\\Z\end{matrix}\right)&=\left(\begin{matrix}Z_y-Y_z\\X_z-Z_x\\Y_x-X_y\end{matrix}\right)\\
\mathrm{div}\left(\begin{matrix}X\\Y\\Z\end{matrix}\right)&=X_x+Y_y+Z_z
\end{aligned}
ディラック作用素を使えば、これらを算出して関係を体系的に整理できます。
\begin{aligned}
&DF=\underbrace{F_x\,dx+F_y\,dy+F_z\,dz}_{d\,≅\,\mathrm{grad}}\\
&D(X\,dx+Y\,dy+Z\,dz)\\
&=\underbrace{X_x+Y_y+Z_z}_{-δ\,≅\,\mathrm{div}}\\
&\quad+\underbrace{(Z_y-Y_z)dy\,dz+(X_z-Z_x)dz\,dx+(Y_x-X_y)dx\,dy}_{d\,≅\,\mathrm{rot}}\\
&D(X\,dy\,dz+Y\,dz\,dx+Z\,dx\,dy)\\
&=\underbrace{(Y_z-Z_y)dx+(Z_x-X_z)dy+(X_y-Y_x)dz}_{-δ\,≅\,-\mathrm{rot}}\\
&\quad+\underbrace{(X_x+Y_y+Z_z)dx\,dy\,dz}_{d\,≅\,\mathrm{div}}\\
&DF\,dx\,dy\,dz=\underbrace{F_x\,dy\,dz+F_y\,dz\,dx+F_z\,dx\,dy}_{-δ\,≅\,\mathrm{grad}}
\end{aligned}
関係を図示します。この図は元ニート2号さんの発案によります。
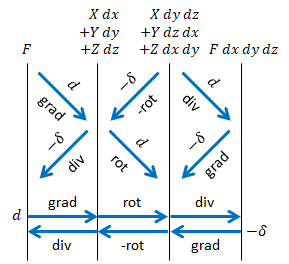
外微分 $d$ と余微分 $-δ$ はほぼ左右対称となっています。rot の符号反転は係数配置の左右反転に由来すると解釈できます。例: $(Z_y-Y_z)\ →\ (Y_z-Z_y)$
この構成は次元によって変化します。実際に計算して確認します。
2次元
計算結果を示します。作用素には添え字で次元を示します。
\begin{aligned}
D(F)&=\underbrace{F_{x}\,dx+F_{y}\,dy}_{d\,≅\,\mathrm{grad}_2}\\
D(X\,dx+Y\,dy)&=\underbrace{X_{x}+Y_{y}}_{-δ\,≅\,\mathrm{div}_2}+\underbrace{(Y_{x}-X_{y})dx\,dy}_{d\,≅\,\mathrm{rot}_2}\\
D(F\,dx\,dy)&=\underbrace{-F_{y}\,dx+F_{x}\,dy}_{-δ\,≅\,\mathrm{grad}_2'}
\end{aligned}
3次元のミニチュア版という印象で、rot や div が小さくて可愛らしいです。2-形式の余微分が不思議な形をしていますが、ホッジ双対が現れています。余微分を考えなければ div を見落とすというのも、ちょっと面白い点です。
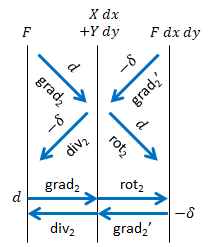
※ 2次元の div や rot は複素解析のコーシー・リーマンの方程式に現れます。👉参考
4次元
$dx,dy,dz$ と同じ性質を持った空間基底 $dw$ を追加します。
基底の並べ方には任意性がありますが、分かりやすさを考慮して3次元の基底の組の前に $dw$ を付けたものを追加します。

計算結果を示します。左辺の $D()$ 内の2-形式は項の数が多いですが、$dw$ を含む基底の係数は黒板太字 $\mathbb{X},\mathbb{Y},\mathbb{Z}$ で示します。
\begin{array}{l}
D(F)=\underbrace{F_{w}\,dw+F_{x}\,dx+F_{y}\,dy+F_{z}\,dz}_{d\,≅\,\mathrm{grad}_4}\\
D(W\,dw+X\,dx+Y\,dy+Z\,dz)\\
=\underbrace{W_{w}+X_{x}+Y_{y}+Z_{z}}_{-δ\,≅\,\mathrm{div}_4}\\
\quad\underbrace{
\begin{aligned}
+(X_{w}-W_{x})dw\,dx+(Y_{w}-W_{y})dw\,dy+(Z_{w}-W_{z})dw\,dz\\
+(Z_{y}-Y_{z})dy\,dz+(X_{z}-Z_{x})dz\,dx+(Y_{x}-X_{y})dx\,dy
\end{aligned}}_{d\,≅\,\mathrm{rot}_4}\\
D(\mathbb{X}\,dw\,dx+\mathbb{Y}\,dw\,dy+\mathbb{Z}\,dw\,dz+X\,dy\,dz+Y\,dz\,dx+Z\,dx\,dy)\\
\left.\begin{array}{l}
=\underbrace{-(\mathbb{X}_{x}+\mathbb{Y}_{y}+\mathbb{Z}_{z})dw}_{-\mathrm{div}}\\
\quad\underbrace{
\begin{aligned}
+(\mathbb{X}_{w}-Z_{y}+Y_{z})dx\\
+(\mathbb{Y}_{w}-X_{z}+Z_{x})dy\\
+(\mathbb{Z}_{w}-Y_{x}+X_{y})dz
\end{aligned}}_{∂_w-\mathrm{rot}}
\end{array}\right\}{\scriptsize -δ}\\
\quad\left.\begin{array}{l}
\underbrace{(X_{x}+Y_{y}+Z_{z})dx\,dy\,dz}_{\mathrm{div}}\\
\underbrace{
\begin{aligned}
+(X_{w}-\mathbb{Z}_{y}+\mathbb{Y}_{z})dw\,dy\,dz\\
+(Y_{w}-\mathbb{X}_{z}+\mathbb{Z}_{x})dw\,dz\,dx\\
+(Z_{w}-\mathbb{Y}_{x}+\mathbb{X}_{y})dw\,dx\,dy
\end{aligned}}_{∂_w-\mathrm{rot}}
\end{array}\right\}{\scriptsize d}\\
D(W\,dx\,dy\,dz+X\,dw\,dy\,dz+Y\,dw\,dz\,dx+Z\,dw\,dx\,dy)\\
=\underbrace{
\begin{aligned}
(Z_{y}-Y_{z})dw\,dx+(X_{z}-Z_{x})dw\,dy+(Y_{x}-X_{y})dw\,dz\\
+(W_{x}+X_{w})dy\,dz+(W_{y}+Y_{w})dz\,dx+(W_{z}+Z_{w})dx\,dy
\end{aligned}}_{-δ\,≅\,\mathrm{rot}_4'}\\
\quad\underbrace{+(W_{w}-X_{x}-Y_{y}-Z_{z})dw\,dx\,dy\,dz}_{d\,≅\,\mathrm{div}_4'}\\
D(F\,dw\,dx\,dy\,dz)\\
=\underbrace{F_{w}\,dx\,dy\,dz-F_{x}\,dw\,dy\,dz-F_{y}\,dw\,dz\,dx-F_{z}\,dw\,dx\,dy}_{-δ\,≅\,\mathrm{grad}_4'}
\end{array}
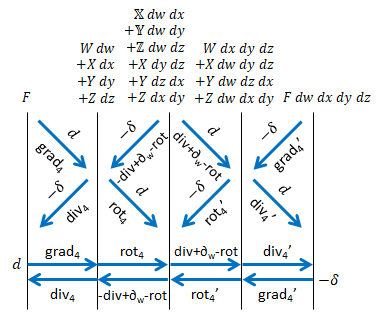
2-形式
2-形式に作用させた結果は非常に複雑です。
添え字で次元を示せば、4次元のディラック作用素 $D_4$ の中に3次元のディラック作用素 $D_3$ が含まれていると解釈することで、構造が分かりやすくなります。
\begin{aligned}
&D_3=d_3-δ_3=dx\frac{∂}{∂x}+dy\frac{∂}{∂y}+dz\frac{∂}{∂z}\\
&D_4=d_4-δ_4=dw\frac{∂}{∂w}+D_3\\
&F=\mathbb{X}\,dx+\mathbb{Y}\,dy+\mathbb{Z}\,dz\\
&G=X\,dy\,dz+Y\,dz\,dx+Z\,dx\,dy\\
&D_4(dw\,F+G)\\
&=\left(dw\frac{∂}{∂w}+D_3\right)(dw\,F+G)\\
&=dw\frac{∂}{∂w}(dw\,F+G)+D_3(dw\,F+G)\\
&=F_w+dw\,G_w-dw\,D_3F+D_3G\\
&=F_w+dw\,G_w-dw\,(d_3-δ_3)F+(d_3-δ_3)G\\
&=\underbrace{dw\overbrace{δ_3F}^{-\mathrm{div}\,F}+F_w-\overbrace{δ_3G}^{\mathrm{rot}\,G}}_{-δ_4}+\underbrace{\overbrace{d_3G}^{\mathrm{div}\,G}+dw(G_w-\overbrace{d_3F}^{\mathrm{rot}\,F})}_{d_4}
\end{aligned}
この結果を直観的に解釈します。4次元2-形式から3次元にない基底 $dw$ を抜いた3次元の1-形式 $F$ と2-形式 $G$ に対して、$w$ での偏微分と $D_3$ を作用させています。
以下の本では2-形式の外微分に相当する作用素を仮に Med と呼んでいます。
\begin{aligned}
\mathrm{Grad}\,F&=\left(\begin{matrix}∂_w\,F \\ \mathrm{grad}\,F\end{matrix}\right)\\
\mathrm{Rot}\left(\begin{matrix}F \\ \mathbf{G}\end{matrix}\right)&=\left(\begin{matrix}-\mathrm{grad}\,F+∂_w\,\mathbf{G} \\ \mathrm{rot}\,\mathbf{G}\end{matrix}\right)\\
\mathrm{Med}\left(\begin{matrix}\mathbf{F} \\ \mathbf{G}\end{matrix}\right)&=\left(\begin{matrix}\mathrm{div}\,\mathbf{G} \\ \mathrm{rot}\,\mathbf{F}-∂_w\,\mathbf{G}\end{matrix}\right)\\
\mathrm{Div}\left(\begin{matrix}F \\ \mathbf{G}\end{matrix}\right)&=∂_w\,F+\mathrm{div}\,\mathbf{G}
\end{aligned}
行列の成分は時間と空間に分離されています。一部符号が異なりますが、どこで違いが生じているかは未確認です。
1次元の時間を含みます。ここでは時間の計量を正、空間の計量を負とします。
4次元
時間1次元+空間3次元です。
\begin{array}{l}
D(F)=\underbrace{F_{t}\,dt+F_{x}\,dx+F_{y}\,dy+F_{z}\,dz}_{d\,≅\,\mathrm{grad}_4}\\
D(T\,dt+X\,dx+Y\,dy+Z\,dz)\\
=\underbrace{T_{t}-X_{x}-Y_{y}-Z_{z}}_{-δ\,≅\,\mathrm{div}_4'}\\
\quad\underbrace{
\begin{aligned}
+(X_{t}-T_{x})dt\,dx+(Y_{t}-T_{y})dt\,dy+(Z_{t}-T_{z})dt\,dz\\
+(Z_{y}-Y_{z})dy\,dz+(X_{z}-Z_{x})dz\,dx+(Y_{x}-X_{y})dx\,dy
\end{aligned}}_{d\,≅\,\mathrm{rot}_4}\\
D(\mathbb{X}\,dt\,dx+\mathbb{Y}\,dt\,dy+\mathbb{Z}\,dt\,dz+X\,dy\,dz+Y\,dz\,dx+Z\,dx\,dy)\\
\left.\begin{array}{l}
=\underbrace{(\mathbb{X}_{x}+\mathbb{Y}_{y}+\mathbb{Z}_{z})dt}_{\mathrm{div}}\\
\quad\underbrace{
\begin{aligned}
+(\mathbb{X}_{t}+Z_{y}-Y_{z})dx\\
+(\mathbb{Y}_{t}+X_{z}-Z_{x})dy\\
+(\mathbb{Z}_{t}+Y_{x}-X_{y})dz
\end{aligned}}_{∂_t+\mathrm{rot}}
\end{array}\right\}{\scriptsize -δ}\\
\quad\left.\begin{array}{l}
\underbrace{+(X_{x}+Y_{y}+Z_{z})dx\,dy\,dz}_{\mathrm{div}}\\
\underbrace{
\begin{aligned}
+(X_{t}-\mathbb{Z}_{y}+\mathbb{Y}_{z})dt\,dy\,dz\\
+(Y_{t}-\mathbb{X}_{z}+\mathbb{Z}_{x})dt\,dz\,dx\\
+(Z_{t}-\mathbb{Y}_{x}+\mathbb{X}_{y})dt\,dx\,dy
\end{aligned}}_{∂_t-\mathrm{rot}}
\end{array}\right\}{\scriptsize d}\\
D(T\,dx\,dy\,dz+X\,dt\,dy\,dz+Y\,dt\,dz\,dx+Z\,dt\,dx\,dy)\\
=\underbrace{
\begin{aligned}
(Y_{z}-Z_{y})dt\,dx+(Z_{x}-X_{z})dt\,dy+(X_{y}-Y_{x})dt\,dz\\
+(X_{t}-T_{x})dy\,dz+(Y_{t}-T_{y})dz\,dx+(Z_{t}-T_{z})dx\,dy
\end{aligned}}_{-δ\,≅\,\mathrm{rot}_4'}\\
\quad\underbrace{+(T_{t}-X_{x}-Y_{y}-Z_{z})dt\,dx\,dy\,dz}_{d\,≅\,\mathrm{div}_4'}\\
D(F\,dt\,dx\,dy\,dz)\\
=\underbrace{F_{t}\,dx\,dy\,dz+F_{x}\,dt\,dy\,dz+F_{y}\,dt\,dz\,dx+F_{z}\,dt\,dx\,dy}_{-δ\,≅\,\mathrm{grad}_4}
\end{array}
ユークリッド空間とは一部の符号が異なりますが、grad や div の形が外微分と余微分で共通しているため、むしろこちらの方がきれいにも見えます。

マクスウェル方程式は係数を変えるだけで導出できます。
\begin{array}{l}
D(φ\,dt-\vec{A}_x\,dx-\vec{A}_y\,dy-\vec{A}_z\,dz)\\
=\underbrace{
φ_{,t}+\vec{A}_{x,x}+\vec{A}_{y,y}+\vec{A}_{z,z}
}_{\frac{∂φ}{∂t}+\mathrm{div}\,\vec{A}=0}\\
\quad+\underbrace{
(-\vec{A}_{x,t}-φ_{,x})dt\,dx
+(-\vec{A}_{y,t}-φ_{,y})dt\,dy
+(-\vec{A}_{z,t}-φ_{,z})dt\,dz
}_{-\frac{∂\vec{A}}{∂t}-\mathrm{grad}\,φ=:\vec{E}}\\
\quad+\underbrace{
(-\vec{A}_{z,y}+\vec{A}_{y,z})dy\,dz
+(-\vec{A}_{x,z}+\vec{A}_{z,x})dz\,dx
+(-\vec{A}_{y,x}+\vec{A}_{x,y})dx\,dy
}_{-\mathrm{rot}\,\vec{A}=:-\vec{B}}\\
=\vec{E}_x\,dt\,dx+\vec{E}_y\,dt\,dy+\vec{E}_z\,dt\,dz-\vec{B}_x\,dy\,dz-\vec{B}_y\,dz\,dx-\vec{B}_z\,dx\,dy\\
\\
D(\vec{E}_x\,dt\,dx+\vec{E}_y\,dt\,dy+\vec{E}_z\,dt\,dz-\vec{B}_x\,dy\,dz-\vec{B}_y\,dz\,dx-\vec{B}_z\,dx\,dy)\\
=\underbrace{
(\vec{E}_{x,x}+\vec{E}_{y,y}+\vec{E}_{z,z})dt
}_{\mathrm{div}\,\vec{E}=:ρ}\\
\quad\underbrace{
\begin{aligned}
&+(\vec{E}_{x,t}-\vec{B}_{z,y}+\vec{B}_{y,z})dx\\
&+(\vec{E}_{y,t}-\vec{B}_{x,z}+\vec{B}_{z,x})dy\\
&+(\vec{E}_{z,t}-\vec{B}_{y,x}+\vec{B}_{x,y})dz
\end{aligned}
}_{\frac{∂\vec{E}}{∂t}-\mathrm{rot}\,\vec{B}=:-\vec{j}}\\
\quad\underbrace{
+(-\vec{B}_{x,x}-\vec{B}_{y,y}-\vec{B}_{z,z})dx\,dy\,dz
}_{\mathrm{div}\,\vec{B}=0}\\
\quad\underbrace{
\begin{aligned}
+(-\vec{B}_{x,t}-\vec{E}_{z,y}+\vec{E}_{y,z})dt\,dy\,dz\\
+(-\vec{B}_{y,t}-\vec{E}_{x,z}+\vec{E}_{z,x})dt\,dz\,dx\\
+(-\vec{B}_{z,t}-\vec{E}_{y,x}+\vec{E}_{x,y})dt\,dx\,dy
\end{aligned}
}_{\frac{∂\vec{B}}{∂t}+\mathrm{rot}\,\vec{E}=0}
\end{array}
詳細はこちらの記事を参照してください。




