【お知らせ】プログラミング記事の投稿はQiitaに移行しました。

内積の視覚化

数学

ベクトルの内積を視覚的に考えます。

語り尽くされたテーマですが、シンプルな説明を心掛けました。

目次

計算

数の組として表される2本のベクトルの間で定義される標準的な内積は、同じ位置の成分を掛けて足したものです。

数ベクトル空間の標準内積の計算方法
\left(\begin{matrix}a_1\\a_2\\\vdots\\a_n\end{matrix}\right) ⋅\left(\begin{matrix}b_1\\b_2\\\vdots\\b_n\end{matrix}\right) =a_1b_1+a_2b_2+\cdots+a_nb_n

内積の視覚的なイメージについて、2次元を例に説明します。

2次元での内積

ベクトルの基礎的な事柄を復習します。既にご存知の方は視覚化に進んでください。

ベクトルの長さ

ベクトルを三角形で考えます。

f:id:n7shi:20180805005240p:plain

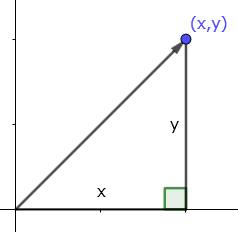
このベクトルを $\vec v$ とします。

\vec v=\left(\begin{matrix}x\\y\end{matrix}\right)

ベクトルの長さを $|\vec v|$ と表記します。ベクトルの長さは三角形の斜辺の長さなので、ピタゴラスの定理から求まります。

ベクトルの長さ
|\vec v|=\sqrt{x^2+y^2}

極座標表示

ベクトルの成分は、ベクトルの長さ $|\vec v|$ と $x$ 軸からの角度 $θ$ でも表現できます。

$|\vec v|>1$ として図示します。円は半径 1 の単位円です。

f:id:n7shi:20180805005534p:plain

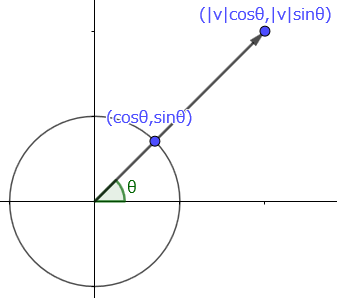
【注意】ベクトルは原点から出ています。単位円との交点 $(\cosθ,\sinθ)$ はベクトルの途中に置かれた点です。

\vec v=|\vec v|\left(\begin{matrix}\cosθ\\\sinθ\end{matrix}\right)

$|\vec v|>1$ 以外の状況は以下の通りです。

  1. $|\vec v|=1$ のとき、ベクトルは単位円上の点を指します。
  2. $|\vec v|<1$ のとき、ベクトルは単位円の内側に納まるため、単位円とは交差しません。

内積

内積を計算します。

\vec A⋅\vec B =\left(\begin{matrix}a_1\\a_2\end{matrix}\right) ⋅\left(\begin{matrix}b_1\\b_2\end{matrix}\right) =a_1b_1+a_2b_2

この意味を視覚化する準備として、内積を極座標表示で計算します。

f:id:n7shi:20180805005653p:plain
\begin{aligned} \vec A⋅\vec B &=|\vec A|\left(\begin{matrix}\cos{(θ+θ_b)}\\\sin{(θ+θ_b)}\end{matrix}\right) ⋅|\vec B|\left(\begin{matrix}\cos{θ_b}\\\sin{θ_b}\end{matrix}\right) \\ &=|\vec A||\vec B|(\cos{(θ+θ_b)}\cos{θ_b}+\sin{(θ+θ_b)}\sin{θ_b}) \\ &=|\vec A||\vec B|\cos\{(θ+θ_b)-θ_b\} \\ &=|\vec A||\vec B|\cosθ \end{aligned}

加法定理を使いました。

加法定理
\begin{aligned} \cos(α+β)&=\cosα\cosβ-\sinα\sinβ \\ \cos(α-β)&=\cosα\cosβ+\sinα\sinβ \end{aligned}

まとめ

ここまでの結果をまとめます。

2次元の内積の計算方法
\vec A⋅\vec B =|\vec A||\vec B|\cosθ =a_1b_1+a_2b_2

$\cosθ$ について整理すれば、内積を長さの積で割った値となります。

角度と内積の関係
\cosθ=\frac{\vec A⋅\vec B}{|\vec A||\vec B|}

視覚化

ベクトルの内積を視覚的に表すと、2本のベクトルの向きを揃えて長さを掛けた値となります。向きを揃えるには垂線を引いて交点を求めます。

簡単な例で確認します。

ベクトル $\vec A,\ \vec B$ を定義します。

\vec A=\left(\begin{matrix}2\\2\end{matrix}\right),\ \vec B=\left(\begin{matrix}3\\0\end{matrix}\right)

後で比較するため、あらかじめ内積を計算しておきます。

\vec A⋅\vec B=\left(\begin{matrix}2\\2\end{matrix}\right)⋅\left(\begin{matrix}3\\0\end{matrix}\right)=2⋅3+2⋅0=6

パターン 1

$\vec A$ を $\vec B$ の向きに揃えます。

$\vec A$ から $\vec B$ に垂線を下ろします。

f:id:n7shi:20180805005752p:plain

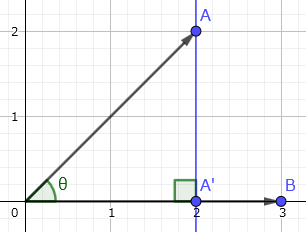
【注意】ベクトルはすべて原点から出ています。垂線との交点 $A'$ は $\vec B$ の途中に置かれた点です。

原点から交点 $A'$ までのベクトルを $\vec A'$ とします。$\vec A$ に上から光を当てて $\vec B$ に映った影というイメージで、$\vec A'$ は $\vec B$ への射影と呼びます。垂線は光の方向に相当します。

\vec A'=\left(\begin{matrix}2\\0\end{matrix}\right)

$\vec A'$ と $\vec B$ の長さを掛ければ、事前に求めた $\vec A$ と $\vec B$ の内積と一致します。

|\vec A'||\vec B|=2⋅3=6=\vec A⋅\vec B

図を見ると次のように $\vec A'$ の長さが表せることが分かります。

|\vec A'|=|\vec A|\cosθ

これを使えば内積の計算方法と一致します。

|\vec A'||\vec B|=|\vec A||\vec B|\cosθ

パターン 2

$\vec B$ を $\vec A$ の向きに揃えます。

$\vec B$ から $\vec A$ に垂線を下ろします。

f:id:n7shi:20180805005912p:plain

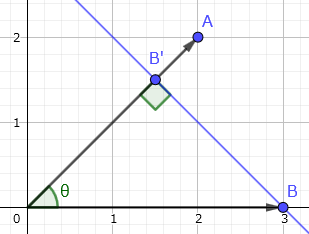
【注意】ベクトルはすべて原点から出ています。垂線との交点 $B'$ は $\vec A$ の途中に置かれた点です。

原点から交点 $B'$ までのベクトルを $\vec B'$ とします。垂線は光の方向を表すことから $\vec A$ への射影をイメージしてください。

\vec B'=\left(\begin{matrix}1.5\\1.5\end{matrix}\right)

$\vec A$ と $\vec B'$ の長さを掛ければ、事前に求めた $\vec A$ と $\vec B$ の内積と一致します。

|\vec A||\vec B'|=\sqrt{2^2+2^2}\sqrt{\left(\frac32\right)^2+\left(\frac32\right)^2}=\sqrt{8⋅\frac92}=6=\vec A⋅\vec B

図を見ると次のように $\vec B'$ の長さが表せることが分かります。

|\vec B'|=|\vec B|\cosθ

これを使えば内積の計算方法と一致します。

|\vec A||\vec B'|=|\vec A||\vec B|\cosθ

まとめ

以上で見たように、内積は $\vec A$ と $\vec B$ どちらの向きに合わせても同じ値が得られます。

原点から垂線との交点までの長さを求める操作が、三角形の斜辺から底辺を求める操作となり、斜辺と底辺が $\cosθ$ で変換されるためです。

f:id:n7shi:20180805005932p:plain

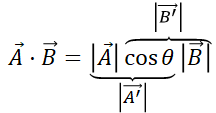
内積は2本のベクトルからスカラーを生成します。ベクトルは向きと大きさを持ちますが、スカラーでは向きが失われて大きさだけが残ります。ベクトルの向きを揃えることで、向きが失われる（次元が1次元に落ちる）と解釈できます。

内積の性質

射影のイメージを持てば、内積の性質が直観的に把握できます。

成分分解

射影の基準となるベクトルが長さ 1 の単位ベクトルであれば、内積は射影されたベクトルの長さとなるため、射影された方向への成分分解となります。

$x$ 軸方向への単位ベクトルにより $x$ 成分を取り出す例です。

\left(\begin{matrix}x\\y\end{matrix}\right) ⋅\left(\begin{matrix}1\\0\end{matrix}\right) =x⋅1+y⋅0 =x

角度の変化

ベクトルの長さを固定したまま角度を変化させてみます。

f:id:n7shi:20180805162721p:plain
\vec A⋅\vec B=|\vec A||\vec B|\cosθ=|\vec A'||\vec B|

角度を大きくすれば内積は減少して、直交した時に 0 となります。

角度を小さくすれば内積は増大して、同じ方向を向いた時に最大となり、長さの積となります。

ノルム

同じ方向の特別な場合として、自分自身との内積は長さの2乗となります。

\vec A⋅\vec A=|\vec A|^2

自分自身との内積によって定義された長さを内積が定めるノルムと呼びます。

内積の交換

演算の順序に依存した計算がないため、内積は交換します。

\vec A⋅\vec B =a_1b_1+a_2b_2 =b_1a_1+b_2a_2 =\vec B⋅\vec A

余弦定理

内積の導入に余弦定理が使われるのが一般的ですが、逆に内積から余弦定理を導くこともできます。

f:id:n7shi:20180805172616p:plain
\begin{aligned} |\vec C|^2 &=|\vec A-\vec B|^2 \\ &=(\vec A-\vec B)⋅(\vec A-\vec B) \\ &=\vec A⋅\vec A-2\,\vec A⋅\vec B+\vec B⋅\vec B \\ &=|\vec A|^2+|\vec B|^2-2|\vec A||\vec B|\cosθ \end{aligned}

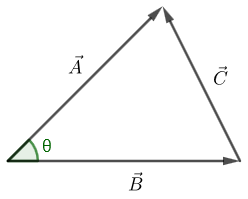
$θ$ が直角なら直角三角形です。$\vec A⋅\vec B=0$ よりピタゴラスの定理となります。

|\vec C|^2=|\vec A|^2+|\vec B|^2

参考

Wikipedia を参考にしました。

謝辞

名前OS@エルフ数学徒さんよりアドバイスを頂きました。

リンク

同じテーマを扱った記事です。

GeoGebra

図形は GeoGebra で作成しました。

www.geogebra.org