複素数でラプラシアンの平方根としてディラック作用素を考えます。
シリーズの記事です。
- 正則関数と反正則関数
- 複素数とディラック作用素 ← この記事
目次
概要
複素数では $z,\bar z$ の微分作用素を次のように定義します。
\begin{aligned}
\frac∂{∂z}&=\frac12\left(\frac∂{∂x}-i\frac∂{∂y}\right) \\
\frac∂{∂\bar z}&=\frac12\left(\frac∂{∂x}+i\frac∂{∂y}\right)
\end{aligned}
これらを組み合わせればラプラシアンになります。
\begin{aligned}
4\frac∂{∂z}\frac∂{∂\bar z}
&=\left(\frac∂{∂x}-i\frac∂{∂y}\right)\left(\frac∂{∂x}+i\frac∂{∂y}\right)
=\frac{∂^2}{∂x^2}+\frac{∂^2}{∂y^2} \\
4\frac∂{∂\bar z}\frac∂{∂z}
&=\left(\frac∂{∂x}+i\frac∂{∂y}\right)\left(\frac∂{∂x}-i\frac∂{∂y}\right)
=\frac{∂^2}{∂x^2}+\frac{∂^2}{∂y^2}
\end{aligned}
この関係を「分岐してから合流する」と捉えて図示します。この菱形表現は元ニート2号さんの発案によります。
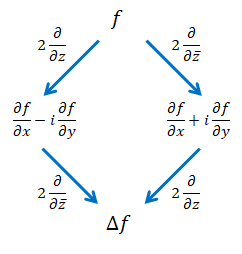
逆に見れば、ラプラシアンの因数分解となります。
\frac{∂^2}{∂x^2}+\frac{∂^2}{∂y^2}
=\left(\frac∂{∂x}+i\frac∂{∂y}\right)\left(\frac∂{∂x}-i\frac∂{∂y}\right)
今回は別の分解としてラプラシアンの2種類の平方根を導きます。
\frac{∂^2}{∂x^2}+\frac{∂^2}{∂y^2}
=\left(dz\frac∂{∂z}+d\bar z\frac∂{∂\bar z}\right)^2
=\left(dx\frac∂{∂x}+dy\frac∂{∂y}\right)^2
ラプラシアンの平方根はディラック作用素と呼ばれます。
方法 1
$\frac∂{∂z}$ と $\frac∂{∂\bar z}$ のクロスタームからラプラシアンが構築されることから、それらに未知の係数 $ε,ε'$ を付けて2乗してみます。
\left(2ε\frac∂{∂z}+2ε'\frac∂{∂\bar z}\right)^2
=4ε^2\frac{∂^2}{∂z^2}+4εε'\frac{∂^2}{∂z∂\bar z}+4ε'ε\frac{∂^2}{∂\bar z∂z}+4{ε'}^2\frac{∂^2}{∂\bar z^2}
偏微分の順序交換を認めます。
=4ε^2\frac{∂^2}{∂z^2}+4(εε'+ε'ε)\frac{∂^2}{∂z∂\bar z}+4{ε'}^2\frac{∂^2}{∂\bar z^2}
これがラプラシアンとなるためには、以下の関係が必要です。
ε^2={ε'}^2=0\ ,\quad εε'+ε'ε=1
このような $ε,ε'$ は複素数としては存在しません。そこでこれを定義として複素数とは別の数として導入します。2乗して $0$ になる数は二重数と呼ばれます。
以上よりラプラシアンの平方根としてディラック作用素 $D$ を定義します。
D:=2ε\frac∂{∂z}+2ε'\frac∂{∂\bar z}
D^2=\frac{∂^2}{∂x^2}+\frac{∂^2}{∂y^2}
行列表現
$ε,ε'$ の行列表現を考えます。
今まで出て来た条件を並べます。
ε^2={ε'}^2=0\ ,\quad εε'+ε'ε=1
求める行列を2行2列と仮定して、$1$ は単位行列とします。
ε^2={ε'}^2=\begin{pmatrix}0&0\\0&0\end{pmatrix}
\ ,\quad
εε'+ε'ε=\begin{pmatrix}1&0\\0&1\end{pmatrix}
成分を $0,1$ に限定してこれらの条件を満たす行列を探します。
from sympy import *
items = [0, 1]
m0 = Matrix([[0, 0], [0, 0]])
m1 = Matrix([[1, 0], [0, 1]])
ms = []
for a in items:
for b in items:
for c in items:
for d in items:
x = Matrix([[a,b], [c,d]])
if x * x == m0:
ms += [x]
for a in ms:
for b in ms:
if a * b + b * a == m1:
print(a, b)
次の2つの組み合わせが見付かりました。
\begin{aligned}
ε &=\begin{pmatrix}0&0\\1&0\end{pmatrix}\ ,&
ε'&=\begin{pmatrix}0&1\\0&0\end{pmatrix} \\
ε &=\begin{pmatrix}0&1\\0&0\end{pmatrix}\ ,&
ε'&=\begin{pmatrix}0&0\\1&0\end{pmatrix}
\end{aligned}
これは順番が異なるだけで、後は決めの問題です。$ε,ε'$ が上三角、下三角となる組み合わせを採用します。
ε =\begin{pmatrix}0&1\\0&0\end{pmatrix}\ ,\quad
ε'=\begin{pmatrix}0&0\\1&0\end{pmatrix}
ディラック作用素の行列表現を求めます。
\begin{aligned}
D&=2ε\frac∂{∂z}+2ε'\frac∂{∂\bar z} \\
&=2\begin{pmatrix}0&1\\0&0\end{pmatrix}\frac∂{∂z}
+2\begin{pmatrix}0&0\\1&0\end{pmatrix}\frac∂{∂\bar z} \\
&=2\begin{pmatrix}0&\frac∂{∂z}\\0&0\end{pmatrix}
+2\begin{pmatrix}0&0\\\frac∂{∂\bar z}&0\end{pmatrix} \\
&=2\begin{pmatrix}0&\frac∂{∂z}\\\frac∂{∂\bar z}&0\end{pmatrix}
\end{aligned}
作用する様子を確認します。$I$ は単位行列です。
\begin{aligned}
Df
&=2\begin{pmatrix}0&\frac∂{∂z}\\\frac∂{∂\bar z}&0\end{pmatrix}f \\
&=2\begin{pmatrix}0&\frac{∂f}{∂z}\\\frac{∂f}{∂\bar z}&0\end{pmatrix} \\
D^2f
&=4\begin{pmatrix}0&\frac∂{∂z}\\\frac∂{∂\bar z}&0\end{pmatrix}
\begin{pmatrix}0&\frac{∂f}{∂z}\\\frac{∂f}{∂\bar z}&0\end{pmatrix} \\
&=4\begin{pmatrix}\frac{∂^2f}{∂z∂\bar z}&0\\0&\frac{∂^2f}{∂\bar z∂z}\end{pmatrix} \\
&=\left(\frac{∂^2f}{∂x^2}+\frac{∂^2f}{∂y^2}\right)I
\end{aligned}
$f$ が分岐して $\frac∂{∂z}$ と $\frac∂{∂\bar z}$ が別々に作用した後、合流してラプラシアンになると解釈できます。
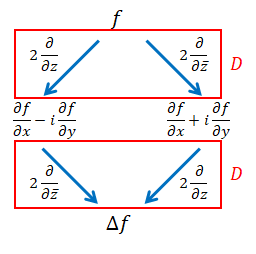
関数 $f$ にディラック作用素を適用します。
Df=2ε\frac{∂f}{∂z}+2ε'\frac{∂f}{∂\bar z}
これは全微分と同じ形です。
df=\frac{∂f}{∂z}dz+\frac{∂f}{∂\bar z}d\bar z
このことから $2ε,2ε'$ を $dz,d\bar z$ と同一視できます。どちらも無限小を表しているためイメージが近いです。
ただし $D$ と $d$ は演算として等価ではありません。$D ^ 2$ はラプラシアンですが、$d$ を外微分とすれば $d ^ 2=0$ です。
そのため同一視するとすれば、$D$ の作用として $dz\,d\bar z+d\bar z\,dz=4$ というルールで扱うと決めます。
D=dz\frac∂{∂z}+d\bar z\frac∂{∂\bar z}
方法 2
2階微分の平方根は1階微分になると推測されます。1階微分に未知の係数 $α,β$ を付けて2乗してみます。
\left(α\frac∂{∂x}+β\frac∂{∂y}\right)^2
=α^2\frac{∂^2}{∂x^2}+αβ\frac{∂^2}{∂x∂y}+βα\frac{∂^2}{∂y∂x}+β^2\frac{∂^2}{∂y^2}
偏微分の順序交換を認めます。
=α^2\frac{∂^2}{∂x^2}+(αβ+βα)\frac{∂^2}{∂x∂y}+β^2\frac{∂^2}{∂y^2}
これがラプラシアンとなるためには、以下の関係が必要です。
α^2=β^2=1\ ,\quad αβ+βα=0
このような $α,β$ は複素数としては存在しません。そこでこれを定義として複素数とは別の数として導入します。このような数はクリフォード数と呼ばれます。
以上よりラプラシアンの平方根としてディラック作用素 $D$ を定義します。
D:=α\frac∂{∂x}+β\frac∂{∂y}
D^2=\frac{∂^2}{∂x^2}+\frac{∂^2}{∂y^2}
クリフォード数
クリフォード数の性質を調べます。
反交換性
αβ+βα=0
を式変形して
αβ=-βα
とすれば、積の順序を交換することで符号が反転していると解釈できます。
これを反交換性と呼びます。
$αβ$ と $βα$ を2乗します。反交換性に注意します。
\begin{aligned}
(αβ)^2&=α\underbrace{βα}_{-αβ}β=-\underbrace{αα}_1\underbrace{ββ}_1=-1 \\
(βα)^2&=β\underbrace{αβ}_{-βα}α=-\underbrace{ββ}_1\underbrace{αα}_1=-1
\end{aligned}
$αβ$ と $βα$ は2乗すると $-1$ になるため虚数単位と同一視できます。ただし係数とは別の空間のため、係数に出て来る $i$ と相互作用することはありません。そのためここでは区別して $γ$ と書きます。$αβ,βα$ には $±γ$ の任意性がありますが、決めの問題として次のように割り当てます。
αβ=-βα=γ
このようにすれば $αβ$ は虚数単位 $γ$ を因数分解したものだと見なせます。
行列表現
$α,β$ の行列表現を考えます。
今まで出て来た条件を並べます。
α^2=β^2=1\ ,\quad αβ=-βα=γ
$1$ と $γ$ を複素数の行列表現にします。👉参考
α^2=β^2=\begin{pmatrix}1&0\\0&1\end{pmatrix}
\ ,\quad
αβ=-βα=\begin{pmatrix}0&-1\\1&0\end{pmatrix}
成分を $0,±1$ に限定してこれらの条件を満たす行列を探します。
from sympy import *
items = [0, 1, -1]
m1 = Matrix([[1, 0], [0, 1]])
mi = Matrix([[0,-1], [1, 0]])
ms = []
for a in items:
for b in items:
for c in items:
for d in items:
x = Matrix([[a,b], [c,d]])
if x * x == m1:
ms += [x]
for a in ms:
for b in ms:
if a * b == mi and b * a == -mi:
print(a, b)
次の4つの組み合わせが見付かりました。
\begin{aligned}
α&=\begin{pmatrix}0&1\\1&0\end{pmatrix}\ ,&
β&=\begin{pmatrix}1&0\\0&-1\end{pmatrix} \\
α&=\begin{pmatrix}0&-1\\-1&0\end{pmatrix}\ ,&
β&=\begin{pmatrix}-1&0\\0&1\end{pmatrix} \\
α&=\begin{pmatrix}1&0\\0&-1\end{pmatrix}\ ,&
β&=\begin{pmatrix}0&-1\\-1&0\end{pmatrix} \\
α&=\begin{pmatrix}-1&0\\0&1\end{pmatrix}\ ,&
β&=\begin{pmatrix}0&1\\1&0\end{pmatrix}
\end{aligned}
後は決めの問題なので、$α$ が一番単純な形となる組み合わせを採用します。
α=\begin{pmatrix}0&1\\1& 0\end{pmatrix}\ ,\quad
β=\begin{pmatrix}1&0\\0&-1\end{pmatrix}
これはパウリ行列の $σ _ 1$ と $σ _ 3$ です。
σ_1=\begin{pmatrix}0& 1\\1& 0\end{pmatrix}\ ,\quad
σ_2=\begin{pmatrix}0&-i\\i& 0\end{pmatrix}\ ,\quad
σ_3=\begin{pmatrix}1& 0\\0&-1\end{pmatrix}
ディラック作用素の行列表現を求めます。
\begin{aligned}
D&=α\frac∂{∂x}+β\frac∂{∂y} \\
&=\begin{pmatrix}0&1\\1& 0\end{pmatrix}\frac∂{∂x}
+\begin{pmatrix}1&0\\0&-1\end{pmatrix}\frac∂{∂y} \\
&=\begin{pmatrix}0&\frac∂{∂x}\\\frac∂{∂x}& 0\end{pmatrix}
+\begin{pmatrix}\frac∂{∂y}&0\\0&-\frac∂{∂y}\end{pmatrix} \\
&=\begin{pmatrix}\frac∂{∂y}&\frac∂{∂x}\\\frac∂{∂x}&-\frac∂{∂y}\end{pmatrix}
\end{aligned}
作用する様子を確認します。$I$ は単位行列です。
\begin{aligned}
Df
&=\begin{pmatrix}\frac∂{∂y}&\frac∂{∂x}\\\frac∂{∂x}&-\frac∂{∂y}\end{pmatrix}f \\
&=\begin{pmatrix}\frac{∂f}{∂y}&\frac{∂f}{∂x}\\\frac{∂f}{∂x}&-\frac{∂f}{∂y}\end{pmatrix} \\
D^2f
&=\begin{pmatrix}\frac∂{∂y}&\frac∂{∂x}\\\frac∂{∂x}&-\frac∂{∂y}\end{pmatrix}
\begin{pmatrix}\frac{∂f}{∂y}&\frac{∂f}{∂x}\\\frac{∂f}{∂x}&-\frac{∂f}{∂y}\end{pmatrix} \\
&=\begin{pmatrix}
\frac{∂^2f}{∂y^2}+\frac{∂^2f}{∂x^2}&\frac{∂^2f}{∂y∂x}-\frac{∂^2f}{∂x∂y} \\
\frac{∂^2f}{∂x∂y}-\frac{∂^2f}{∂y∂x}&\frac{∂^2f}{∂x^2}+\frac{∂^2f}{∂y^2}
\end{pmatrix} \\
&=\begin{pmatrix}
\frac{∂^2f}{∂x^2}+\frac{∂^2f}{∂y^2}&0 \\
0&\frac{∂^2f}{∂x^2}+\frac{∂^2f}{∂y^2}
\end{pmatrix} \\
&=\left(\frac{∂^2f}{∂x^2}+\frac{∂^2f}{∂y^2}\right)I
\end{aligned}
$f$ が分岐して $\frac∂{∂x}$ と $\frac∂{∂y}$ が別々に作用した後、合流してラプラシアンになると解釈できます。
$α,β,γ$ の組み合わせで生成される代数は分解型四元数と呼ばれるものです。
英語版 Wikipedia の記事(split quaternion)に以下の行列計算が載っています。
\begin{pmatrix}0&1\\1&0\end{pmatrix}
\begin{pmatrix}1&0\\0&-1\end{pmatrix}
=\begin{pmatrix}0&-1\\1&0\end{pmatrix}
これは $αβ=γ$ です。$α$ が $β$ の上下を入れ替えて $γ$ になっています。
分解型四元数は $i,j,k$ の文字で表記します。$i ^ 2=-1,\ ij=k$ が基本構造です。対応するのは $γ ^ 2=-1,\ γβ=α$ です。まとめると次の通りです。
\{i,j,k\}≅\{γ,β,α\}
関数 $f$ にディラック作用素を適用します。
Df=α\frac{∂f}{∂x}+β\frac{∂f}{∂y}
これは全微分と同じ形です。
df=\frac{∂f}{∂x}dx+\frac{∂f}{∂y}dy
このことから $α,β$ を $dx,dy$ と同一視できます。
ただし $D$ と $d$ は演算として等価ではありません。$D ^ 2$ はラプラシアンですが、$d$ を外微分とすれば $d ^ 2=0$ です。
そのため同一視するとすれば、$D$ の作用として $dx,dy$ をクリフォード数として扱うと決めます。
D=dx\frac∂{∂x}+dy\frac∂{∂y}
まとめ
ここまでの結果を図にまとめます。
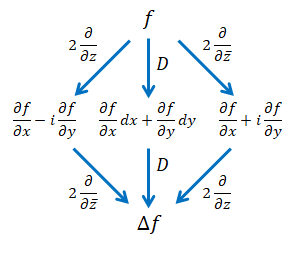
ディラック作用素は別ルートでラプラシアンに至っています。分解型四元数によって別ルートを開拓しています。
統合
$ε,ε'$ と $α,β$ は別々に扱って来ました。$ε,ε'$ を $α,β$ で表すことで統合を試みます。
全微分より以下の同一性を仮定します。
\begin{aligned}
dz,d\bar z&≅2ε,2ε' \\
dx,dy&≅α,β
\end{aligned}
これによって複素解析の関係式を書き直します。
\begin{aligned}
d z&=dx+i\,dy &&⇒& 2ε &=α+iβ \\
d\bar z&=dx-i\,dy &&⇒& 2ε'&=α-iβ
\end{aligned}
$ε,ε'$ と $α,β$ は次の関係式を満たします。
\begin{aligned}
ε^2={ε'}^2=0\ &,\quad εε'+ε'ε=1 \\
α^2=β^2=1\ &,\quad αβ=-βα=γ
\end{aligned}
$ε,ε'$ を $α,β$ で表して、定数倍した $ε,ε'$ の関係式を満たすか確認します。
(2ε)^2=(2ε')^2=0\ ,\quad 4εε'+4ε'ε=4
\begin{aligned}
(2ε )^2&=(α+iβ)^2=α^2+iαβ+iβα-β^2=1+iγ-iγ-1=0 \\
(2ε')^2&=(α-iβ)^2=α^2-iαβ-iβα-β^2=1-iγ+iγ-1=0 \\
4εε'+4ε'ε
&=(α+iβ)(α-iβ)+(α-iβ)(α+iβ) \\
&=(α^2-iαβ+iβα+β^2)+(α^2+iαβ-iβα+β^2) \\
&=(1-iγ-iγ+1)+(1+iγ+iγ+1) \\
&=4
\end{aligned}
うまくいきました。$α±iβ$ が冪零元となっているのが興味深いです。
行列表現
$ε,ε'$ の行列表現を $α,β$ で書き直します。
α=\begin{pmatrix}0&1\\1& 0\end{pmatrix}\ ,\quad
β=\begin{pmatrix}1&0\\0&-1\end{pmatrix}
\begin{aligned}
ε &=\frac12(α+iβ)=\frac12\begin{pmatrix}i&1\\1&-i\end{pmatrix} \\
ε'&=\frac12(α-iβ)=\frac12\begin{pmatrix}-i&1\\1&i\end{pmatrix}
\end{aligned}
ディラック作用素の行列表現を求めます。
\begin{aligned}
D&=2ε\frac∂{∂z}+2ε'\frac∂{∂\bar z} \\
&=\begin{pmatrix}i&1\\1&-i\end{pmatrix}\frac∂{∂z}
+\begin{pmatrix}-i&1\\1&i\end{pmatrix}\frac∂{∂\bar z} \\
&=\begin{pmatrix}
i\frac∂{∂z}-i\frac∂{∂\bar z} &
\frac∂{∂z}+ \frac∂{∂\bar z} \\
\frac∂{∂z}+ \frac∂{∂\bar z} &
-i\frac∂{∂z}+i\frac∂{∂\bar z}
\end{pmatrix}
\end{aligned}
複素解析の関係式を適用します。
\begin{aligned}
\frac∂{∂z}+\frac∂{∂\bar z}&=\frac∂{∂x} \\
\frac∂{∂z}-\frac∂{∂\bar z}&=-i\frac∂{∂y}
\end{aligned}
D=\begin{pmatrix}\frac∂{∂y}&\frac∂{∂x}\\\frac∂{∂x}&-\frac∂{∂y}\end{pmatrix}
$α,β$ で表したディラック作用素の行列表現と一致しました。
まとめ
ラプラシアンの平方根がディラック作用素です。1階の作用は全微分と同一視します。
D=dz\frac∂{∂z}+d\bar z\frac∂{∂\bar z}
=dx\frac∂{∂x}+dy\frac∂{∂y}
D^2=\frac{∂^2}{∂x^2}+\frac{∂^2}{∂y^2}
参考
ディラック作用素は以下の記事を参照してください。
分解型四元数は以下の記事を参照してください。分解型四元数は双四元数の部分代数です。
今回の議論はディラック方程式の簡易版に相当します。ディラック方程式は以下の記事を参照してください。


