分解型複素数の直和分解から固有値を導入します。
『行列と代数系』シリーズの記事です。
- 実二次正方行列の初歩
- 実二次正方行列と代数系
- 冪零行列と二重数
- 三種類の二元数
- 分解型四元数と同型対応
- 分解型四元数と幾何代数
- 行列表現と外積と行列式
- 分解型複素数と固有値 ← この記事
目次
分解型複素数は光円錐上の零因子となる冪等元を基底として直和分解されます。
i'=\frac12(1+j),\ j'=\frac12(1-j)
i'^2=i',\ j'^2=j',\ i'j'=j'i'=0
\begin{aligned}
&(ai'+bj')(ci'+dj')=aci'+bdj' \\
&\mapsto\ (a⊕b)(c⊕d)=ac⊕bd
\end{aligned}

$1,j$ による表示から $i',j'$ による表示への変換は和と差の関係からできます。
i'+j'=1,\ i'-j'=j
a+bj=a(i'+j')+b(i'-j')=(a+b)i'+(a-b)j'
具体例を示します。同じ計算を $1,j$ と $i',j'$ で行います。$i',j'$ で表示することにより積が2つに分解されることが分かります。
\begin{aligned}
&(4+3j)(2+1j)=11+10j \\
&\mapsto\ (7i'+j')(3i'+j')=21i'+j' \\
&\mapsto\ (7⊕1)(3⊕1)=21⊕1
\end{aligned}
直和分解がどのような考え方から出て来るのかを見ます。
任意の分解型複素数に $i'$ を掛けると $i'$ の定数倍が得られます。
\textcolor{red}{(ai'+bj')}i'=\textcolor{red}{a}i'
赤字部分に注目すれば $ai'+bj'→a$ という変化だと見なせます。このように対象($ai'+bj'$)に何か($i'$)を掛けることで、結果がその何かの定数倍($a$ 倍)となる場合、その定数を対象の固有値と呼びます。また、一般的な名称ではありませんが、掛ける何かをここでは固有基底と呼ぶことにします。
対象 × 固有基底 = 固有値 × 固有基底
固有基底が異なれば固有値も異なります。$j'$ を掛ければ $b$ が得られます。
\textcolor{red}{(ai'+bj')}j'=\textcolor{red}{b}j'
このように $ai'+bj'$ の固有値は $a,b$ です。直和分解したときの個々の値が固有値に対応します。
※ 固有値が2つだけなのは後で固有方程式の解から示します。
固有基底を定数倍すると、表される対象を保つために係数はその逆数倍になるため、取り出される固有値は変化しません。
\begin{alignedat}{2}
&\overbrace{\left\{\frac{a}{\textcolor{red}{n}}(\textcolor{red}{n}i')+\frac{b}{\textcolor{red}{m}}(\textcolor{red}{m}j')\right\}}^{ai'+bj'}(\textcolor{red}{n}i')&&=a(\textcolor{red}{n}i') \\
&\left\{\frac{a}{\textcolor{red}{n}}(\textcolor{red}{n}i')+\frac{b}{\textcolor{red}{m}}(\textcolor{red}{m}j')\right\}(\textcolor{red}{m}j')&&=b(\textcolor{red}{m}j')
\end{alignedat}
※ 基底と係数が反比例する関係を共変性・反変性と呼びます。いずれ機会を改めて取り上げる予定です。
このように掛けて固有値を取り出すという点では、固有基底には定数倍の自由度があります。ただし上で見たように任意の分解型複素数を固有基底で表したときの係数は固有基底に依存します。係数が固有値と一致するように選んだのが $i',j'$ です。(詳細は後述)
ここまでは対象を $i',j'$ で表したため係数を取り出しているだけに見えます。対象を $1,j$ で表して計算してみます。
\begin{aligned}
\textcolor{red}{(a+bj)}i'
&=(a+bj)\frac12(1+j) \\
&=\frac12(a+bj+aj+b) \\
&=\frac12\{a(1+j)+b(1+j)\} \\
&=\frac12(a+b)(1+j) \\
&=\textcolor{red}{(a+b)}i'
\end{aligned}
\begin{aligned}
\textcolor{red}{(a+bj)}j'
&=(a+bj)\frac12(1-j) \\
&=\frac12(a+bj-aj-b) \\
&=\frac12\{a(1-j)-b(1-j)\} \\
&=\frac12(a-b)(1-j) \\
&=\textcolor{red}{(a-b)}j'
\end{aligned}
計算した固有値は $1,j$ から $i',j'$ への変換で現れた係数に一致します。
\textcolor{red}{a+bj}=\textcolor{red}{(a+b)}i'+\textcolor{red}{(a-b)}j'
固有方程式
ここまではあらかじめ固有基底 $i',j'$ を知っている所から話を始めましたが、そもそも固有基底が不明な場合に固有値を見付ける方法を考えます。
対象となる分解型複素数を $A=a+bj$、固有基底を $X=c+dj$、固有値を $λ$ とします。$X=0$ だと固有値が決まらないため $X≠0$ とします。
AX=λX\quad(X≠0)
左辺に項を集めます。
(A-λ)X=0
$X≠0$ より $A-λ$ と $X$ は零因子です。分解型複素数では零因子の絶対値は $0$ になることから固有値や固有基底が求まります。
固有値を求める方程式を固有方程式(特性方程式)と呼びます。
固有方程式を解いて固有値を求めます。絶対値を外す際の平方根を避けるため両辺を2乗します。
\begin{aligned}
0
&=|A-λ|^2 \\
&=|a+bj-λ|^2 \\
&=|(a-λ)+bj|^2 \\
&=\{(a-λ)+bj\}\{(a-λ)-bj\} \\
&=(a-λ)^2-b^2 \\
&=a^2-2aλ+λ^2-b^2 \\
&=λ^2-2aλ+a^2-b^2 \\
&=λ^2-2aλ+(a+b)(a-b) \\
&=\{λ-(a+b)\}\{λ-(a-b)\} \\
∴λ&=a+b,\ a-b
\end{aligned}
分解型複素数 $a+bj$ の固有値が $a+b$ と $a-b$ であることが確認できました。
光円錐
同様にして固有基底を求めます。
\begin{aligned}
|X|^2&=|c+dj|^2=c^2-d^2=0 \\
d^2&=c^2 \\
d&=c,\ -c \\
X&=c+cj,\ c-cj \\
∴X&=c(1+j),\ c(1-j)
\end{aligned}
$c$ は固有基底に定数倍の自由度があることを意味します。$c$ を動かすことで、絶対値が $0$ の分解型複素数は原点を中心に X 字形をしていることが分かります。
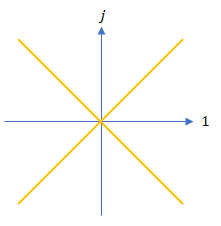
※ この X 字形は特殊相対性理論で光円錐と呼ばれます。
固有基底で任意の分解型複素数を表したときに、係数が固有値(赤字部分)と一致するように $c$ を選びます。
\begin{aligned}
a+bj
&=\textcolor{red}{(a+b)}c(1+j)+\textcolor{red}{(a-b)}c(1-j) \\
&=c\{(a+b+a-b)+(a+b-a+b)j\} \\
&=2c(a+bj) \\
∴c&=\frac12
\end{aligned}
このようにして $i',j'$ が選ばれました。
i'=\frac12(1+j),\ j'=\frac12(1-j)
また、固有方程式 $|A-λ|=0$ は $A$ を左に $λ$ だけずらして光円錐の上に載せることを意味します。下図の赤字部分が固有値です。
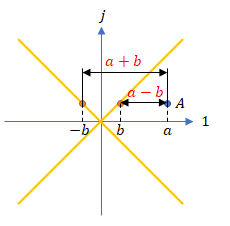
※ この図は固有値が正の場合です。負の場合は右にずらす位置関係になります。
分解型複素数では零因子の性質を使って固有値や固有基底を求めました。しかし複素数には $0$ でない零因子が存在しないため、同じ方法は使えません。行列表現を用いる必要があります。
行列
行列で固有値を考えるには、いくつか概念の導入が必要となります。それらを説明した後で行列の固有値を説明する予定です。
◀前の記事 ▲記事一覧 次の記事▶


