Physics Advent Calendar 2017 7日目の参加記事です。
ディラック作用素でマクスウェル方程式を求めるまでの流れを説明します。計算の道具として使うことを想定して、厳密さには拘らずになるべく直観的に記述します。
この記事は元ニート2号さんにご教示頂いた理論をベースにしています。ここに感謝の意を表します。
【2018.07.26】全面的に改訂しました。
目次
2変数関数を全微分します。
\begin{aligned}
df(x,y)
&=\frac{∂f}{∂x}dx+\frac{∂f}{∂y}dy\\
&=\left(dx\frac{∂}{∂x}+dy\frac{∂}{∂y}\right)f
\end{aligned}
全微分の作用を分離したものをディラック作用素として定義します。
D:=dx\frac{∂}{∂x}+dy\frac{∂}{∂y}
余接ベクトル
$dx,dy$ はベクトル空間の基底となるため、表式はベクトルと同一視できます。
\begin{aligned}
f\,dx+g\,dy&≅\left(\begin{matrix}f\\g\end{matrix}\right)\\
D=dx\frac{∂}{∂x}+dy\frac{∂}{∂y}&≅\left(\begin{matrix}\frac{∂}{∂x} \\ \frac{∂}{∂y}\end{matrix}\right)=\nabla
\end{aligned}
これを余接ベクトルと呼びます。
クリフォード代数
内積と外積を同時に扱う代数系です。積は幾何積と呼びます。
dx^2=dy^2=1\\
dx\,dy=-dy\,dx
前者は内積、後者は外積(ウェッジ積)を表します。外積の関係式は「順序を交換すると符号が反転する」と解釈して反交換性と呼びます。
3つ以上の基底の積を計算する場合、内積を計算するには反交換性を使って隣接させる必要があります。
dx\,\underbrace{dy\,dx}_{\text{交換}}=-\underbrace{dx\,dx}_{1}\,dy=-dy
積に含まれる基底の数をグレードと呼びます。内積によってグレードが下がることを縮約と表現します。
ディラック作用素はラプラシアン(ラプラス作用素)の平方根となるように定義されます。2乗すればラプラシアンを再現します。
\begin{aligned}
D^2
&=D\left(dx\frac{∂}{∂x}+dy\frac{∂}{∂y}\right)\\
&=\left(D\frac{∂}{∂x}\right)dx+\left(D\frac{∂}{∂y}\right)dy\\
&=\left(dx\frac{∂^2}{∂x^2 }+dy\frac{∂^2}{∂y∂x}\right)dx
+\left(dx\frac{∂^2}{∂x∂y}+dy\frac{∂^2}{∂y^2 }\right)dy\\
&=\underbrace{dx^2}_1\frac{∂^2}{∂x^2}+\underbrace{dy^2}_1\frac{∂^2}{∂y^2}+\underbrace{(dx\,dy+dy\,dx)}_0\frac{∂^2}{∂x∂y}\\
&=\frac{∂^2}{∂x^2}+\frac{∂^2}{∂y^2}\\
&=Δ
\end{aligned}
途中でクリフォード代数の関係式を使っています。
ディラック作用素を計算すると、基底が縮約する項としない項に分かれます。これらを分離して、縮約する部分を余微分 $δ$ の符号反転、縮約しない方を外微分 $d$ と呼びます。
余微分が符号反転するのは由来がディラック作用素とは異なるためです。今回はディラック作用素の計算のみを扱うため余微分は常に符号反転して現れます。以降は符号反転とは断らずに余微分と呼びますが、数式では $−δ$ と表記します。
\begin{aligned}
D(X\,dx+Y\,dy)
&=\left(\frac{∂X}{∂x}dx+\frac{∂X}{∂y}dy\right)dx+\left(\frac{∂Y}{∂x}dx+\frac{∂Y}{∂y}dy\right)dy\\
&=\frac{∂X}{∂x}\underbrace{dx\,dx}_{\text{縮約}}+\frac{∂X}{∂y}\underbrace{dy\,dx}_{\text{交換}}+\frac{∂Y}{∂x}dx\,dy+\frac{∂Y}{∂y}\underbrace{dy\,dy}_{\text{縮約}}\\
&=\underbrace{\frac{∂X}{∂x}+\frac{∂Y}{∂y}}_{\text{余
微分}\,-δ}+\underbrace{\left(\frac{∂Y}{∂x}-\frac{∂X}{∂y}\right)dx\,dy}_{\text{外
微分}\,d}
\end{aligned}
この関係を $D=d-δ$ と表現します。幾何積は内積と外積を含みますが、ディラック作用素は係数の全微分と基底との幾何積となり、内積から余微分、外積から外微分が生成されます。
ディラック作用素により余微分と外微分に分岐するとイメージできます。

ラプラシアンは基底を含まないことからグレードを変えません。これは連続した外微分や余微分が 0 になるためです。
dd=δδ=0
一度分岐して、再度収斂することから、菱形としてイメージできます。この図は元ニート2号さんの発案によります。

これを式で表すと次の通りです。
D^2=(d-δ)^2=\underbrace{δδ+dd}_0-dδ-δd=-(dδ+δd)=Δ
時間1次元と空間3次元で構成されます。簡単のため光速を 1 とおいて、ディラック作用素と内積は次のように定義します。内積は空間の計量を表します。異なる基底同士の反交換性は2次元と同様です。
D:=dt\frac{∂}{∂t}+dx\frac{∂}{∂x}+dy\frac{∂}{∂y}+dz\frac{∂}{∂z}
dt^2=1,\ dx^2=dy^2=dz^2=-1
ディラック作用素の2乗はダランベルシアンとなります。
D^2=\frac{∂^2}{∂t^2}-\frac{∂^2}{∂x^2}-\frac{∂^2}{∂y^2}-\frac{∂^2}{∂z^2}=\Box
電磁ポテンシャル
電磁場の源となるベクトル場を電磁ポテンシャルと呼び $A$ と表記します。時間成分はスカラーポテンシャル $φ$、空間成分はベクトルポテンシャル $-\vec{A}$ として含みます。
※ 電磁ポテンシャル $A$ とベクトルポテンシャル $\vec{A}$ は矢印で区別します。
A:=φ\,dt-\vec{A}_x\,dx-\vec{A}_y\,dy-\vec{A}_z\,dz≅\left(\begin{matrix}φ \\ -\vec{A}_x \\ -\vec{A}_y \\ -\vec{A}_z\end{matrix}\right)
電磁ポテンシャルにディラック作用素を適用した $DA$ を計算します。外微分 $dA$ と余微分 $-δA$ が得られます。後で説明する事項も注釈として入れておきます。偏微分の記法は後述します。
\begin{aligned}
DA
&=D(φ\,dt-\vec{A}_x\,dx-\vec{A}_y\,dy-\vec{A}_z\,dz)\\
&\left.\begin{array}{l}
=\underbrace{
φ_{,t}+\vec{A}_{x,x}+\vec{A}_{y,y}+\vec{A}_{z,z}
}_{\frac{∂φ}{∂t}+\mathrm{div}\,\vec{A}=0}
\end{array}\right\}{\scriptsize -δA=0}\\
&\quad\left.\begin{array}{l}
\underbrace{
\begin{aligned}
+(-\vec{A}_{x,t}-φ_{,x})dt\,dx\\
+(-\vec{A}_{y,t}-φ_{,y})dt\,dy\\
+(-\vec{A}_{z,t}-φ_{,z})dt\,dz
\end{aligned}
}_{-\frac{∂\vec{A}}{∂t}-\mathrm{grad}\,φ=:\vec{E}}\\
\underbrace{
\begin{aligned}
+(-\vec{A}_{z,y}+\vec{A}_{y,z})dy\,dz\\
+(-\vec{A}_{x,z}+\vec{A}_{z,x})dz\,dx\\
+(-\vec{A}_{y,x}+\vec{A}_{x,y})dx\,dy
\end{aligned}
}_{-\mathrm{rot}\,\vec{A}=:-\vec{B}}
\end{array}\right\}{\scriptsize dA=:F}\\
\end{aligned}
※ $-δA$ 全体は grad、$dA$ 全体は rot を4次元に拡張した形になっています。その中から3次元成分を切り出して注釈を加えています。

コンマで区切った後の添え字は偏微分を表します。
\begin{aligned}
φ_{,x}&=\frac{∂φ}{∂x}\\
\vec{A}_{x,y}&=\frac{∂\vec{A}_x}{∂y}
\end{aligned}
ゲージ変換
電磁ポテンシャルには $dA$ に影響しない範囲での自由度があります。$dd=0$ より、任意のスカラー場 $χ$ の外微分 $dχ$ が該当します。
\begin{aligned}
A':=&A+dχ\\
dA'=&dA+\underbrace{ddχ}_0=dA
\end{aligned}
このように電磁ポテンシャルを変形する操作をゲージ変換と呼びます。

このような操作は捉え所がないように感じるかもしれません。外微分は微分の一種ですから、微分で消える(0 になる)要素を加えているという意味合いで、とりあえず積分定数 $C$ のようなものだとイメージしておけば良いでしょう。
\begin{aligned}
\int f(x)\,dx&=F(x)+C\\
\int dA&=A+dχ
\end{aligned}
ローレンス条件
ゲージ変換により余微分が $-δA=0$ となるように調整できます。
\frac{∂φ}{∂t}+\mathrm{div} \vec{A}=0
これをローレンス条件と呼びます。ローレンツ条件とも表記されますが、ローレンツ変換のローレンツとは別人で、区別のためローレンスの表記を使用します。

今回対象とする電磁ポテンシャル $A$ はローレンス条件を満たすように調整されているとします。
$dA$ を電磁テンソル $F$ と定義します。これは電磁場の表現で、ファラデーテンソルとも呼ばれます。時間基底の有無で項を分離して、電場 $\vec{E}$ と磁束密度 $-\vec{B}$ に割り当てます。簡単のため誘電率と透磁率は 1 とします。
\begin{aligned}
F:=&dA\\
=&\vec{E}_x\,dt\,dx+\vec{E}_y\,dt\,dy+\vec{E}_z\,dt\,dz
-\vec{B}_x\,dy\,dz-\vec{B}_y\,dz\,dx-\vec{B}_z\,dx\,dy
\end{aligned}
成分を確認します。
\begin{aligned}
\vec{E}
&=\left(\begin{matrix}\vec{E}_x \\ \vec{E}_y \\ \vec{E}_z\end{matrix}\right)
=\left(\begin{matrix}-\vec{A}_{x,t}-φ_{,x} \\ -\vec{A}_{y,t}-φ_{,y} \\ -\vec{A}_{z,t}-φ_{,z}\end{matrix}\right)
=-\frac{∂\vec{A}}{∂t}-\mathrm{grad}\,φ\\
\vec{B}
&=\left(\begin{matrix}\vec{B}_x \\ \vec{B}_y \\ \vec{B}_z\end{matrix}\right)
=\left(\begin{matrix}\vec{A}_{z,y}-\vec{A}_{y,z} \\ \vec{A}_{x,z}-\vec{A}_{z,x} \\ \vec{A}_{y,x}-\vec{A}_{x,y}\end{matrix}\right)
=\mathrm{rot}\,\vec{A}
\end{aligned}
電磁テンソル $F$ にディラック作用素を適用すればマクスウェル方程式が得られます。後で説明する事項も注釈として入れておきます。
\begin{aligned}
DF
&=D(\vec{E}_x\,dt\,dx+\vec{E}_y\,dt\,dy+\vec{E}_z\,dt\,dz-\vec{B}_x\,dy\,dz-\vec{B}_y\,dz\,dx-\vec{B}_z\,dx\,dy)\\
&\left.\begin{array}{l}
=\underbrace{
(\vec{E}_{x,x}+\vec{E}_{y,y}+\vec{E}_{z,z})dt
}_{\mathrm{div}\,\vec{E}=:ρ}\\
\quad\underbrace{
\begin{aligned}
+(\vec{E}_{x,t}-\vec{B}_{z,y}+\vec{B}_{y,z})dx\\
+(\vec{E}_{y,t}-\vec{B}_{x,z}+\vec{B}_{z,x})dy\\
+(\vec{E}_{z,t}-\vec{B}_{y,x}+\vec{B}_{x,y})dz
\end{aligned}
}_{\frac{∂\vec{E}}{∂t}-\mathrm{rot}\,\vec{B}=:-\vec{j}}
\end{array}\right\}{\scriptsize -δF=:J}\\
&\quad\left.\begin{array}{l}
\underbrace{
+(-\vec{B}_{x,x}-\vec{B}_{y,y}-\vec{B}_{z,z})dx\,dy\,dz
}_{\mathrm{div}\,\vec{B}=0}\\
\underbrace{
\begin{aligned}
+(-\vec{B}_{x,t}-\vec{E}_{z,y}+\vec{E}_{y,z})dt\,dy\,dz\\
+(-\vec{B}_{y,t}-\vec{E}_{x,z}+\vec{E}_{z,x})dt\,dz\,dx\\
+(-\vec{B}_{z,t}-\vec{E}_{y,x}+\vec{E}_{x,y})dt\,dx\,dy
\end{aligned}
}_{\frac{∂\vec{B}}{∂t}+\mathrm{rot}\,\vec{E}=0}
\end{array}\right\}{\scriptsize dF=0}\\
\end{aligned}
$dF=ddA=0$ より次の2本の式が得られます。
\left\{\begin{aligned}
\mathrm{div}\,\vec{B}&=0\\
\frac{∂\vec{B}}{∂t}+\mathrm{rot}\,\vec{E}&=0
\end{aligned}\right.
四元電流密度
$-δF$ を四元電流密度 $J$ と定義します。時間成分を電荷密度 $ρ$、空間成分を電流密度 $-\vec{j}$ に割り当てます。
\begin{aligned}
J:=&-δF\\
=&ρdt-\vec{j}_x\,dx-\vec{j}_y\,dy-\vec{j}_z\,dz
\end{aligned}
成分を確認します。
\begin{aligned}
\vec{j}
=\left(\begin{matrix}
\vec{j}_x \\ \vec{j}_y \\ \vec{j}_z
\end{matrix}\right)
=\left(\begin{matrix}
-\vec{E}_{x,t}+\vec{B}_{z,y}-\vec{B}_{y,z}\\
-\vec{E}_{y,t}+\vec{B}_{x,z}-\vec{B}_{z,x}\\
-\vec{E}_{z,t}+\vec{B}_{y,x}-\vec{B}_{x,y}
\end{matrix}\right)
=-\frac{∂\vec{E}}{∂t}+\mathrm{rot}\,\vec{B}
\end{aligned}
これにより残りの2本の式が得られます。
\left\{\begin{aligned}
\mathrm{div}\,\vec{E}&=ρ\\
-\frac{∂\vec{E}}{∂t}+\mathrm{rot}\,\vec{B}&=\vec{j}
\end{aligned}\right.
$-δF=J$ が電荷の流れを表すのと対比すれば、$dF=0$ は磁荷(モノポール)の流れが存在しないということを意味するようです。
まとめ
電磁ポテンシャルからマクスウェル方程式までは一本の式にまとまります。
D^2A=J
$dA=F$ から $\vec{E}$ と $\vec{B}$、$-δF=J$ から $ρ$ と $\vec{j}$ を定義すれば、4本のマクスウェル方程式が得られます。
DF=J \quad
\left\{\begin{array}{r}
dF=0\\\\\\
-δF=J
\end{array}\ \ \right.
\begin{array}{l}
\left\{\begin{array}{r}
\ \ \,\mathrm{div}\,\vec{B}=0\\
\ \ \,\frac{∂\vec{B}}{∂t}+\mathrm{rot}\,\vec{E}=0
\end{array}\right.\\
\left\{\begin{array}{r}
\mathrm{div}\,\vec{E}=ρ\\
-\frac{∂\vec{E}}{∂t}+\mathrm{rot}\,\vec{B}=\vec{j}
\end{array}\right.
\end{array}
関係を図にまとめます。
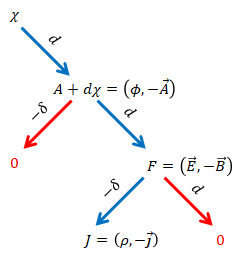
ディラック作用素の二股に分岐する表現がうまく当てはまっていると感じます。
参考
ディラック作用素や余微分の詳細は以下の記事を参照してください。





