恒等変換から単位行列、逆変換から逆行列を定義します。
『行列と代数系』シリーズの記事です。
- 実二次正方行列の初歩
- 一次変数変換と行列の積
- 単位行列と逆行列 ← この記事
- 掃き出し法と逆行列
- 行列の積の性質
- 行列の演算
- ケイリー・ハミルトンの定理
- 零行列と冪零行列
- 零因子ペアの生成
- 実二次正方行列と代数系
目次
次の式は変数 $x,y$ と $x',y'$ が等しいことを表します。
\begin{cases}
x=x' \\
y=y'
\end{cases}
このように何も変化しない変換を恒等変換と呼びます。
行列の形に直すときは各変数に対して係数が必要です。存在しない項は係数 $0$ と見なします。
\begin{cases}
x=1x'+0y' \\
y=0x'+1y'
\end{cases}
恒等変換に対応する行列を単位行列と呼びます。$I$ と表記します。
単位行列
I=\begin{pmatrix}1&0\\0&1\end{pmatrix}
※ $E$ と表記されることもあります。
性質
単位行列に他の行列を掛けても元のままです。
\begin{pmatrix}a&b\\c&d\end{pmatrix}
\begin{pmatrix}1&0\\0&1\end{pmatrix}
=
\begin{pmatrix}1&0\\0&1\end{pmatrix}
\begin{pmatrix}a&b\\c&d\end{pmatrix}
=
\begin{pmatrix}a&b\\c&d\end{pmatrix}
単位行列を $I$ と表記するのは、この性質が $1$ を掛けることに似ているためです。
単位行列の性質
\begin{pmatrix}a&b\\c&d\end{pmatrix}I
=I\begin{pmatrix}a&b\\c&d\end{pmatrix}
=\begin{pmatrix}a&b\\c&d\end{pmatrix}
$x,y$ は別の変数 $x',y'$ の一次式で表されるとします。
\tag{1}
\begin{cases}
x=ax'+by' \\
y=cx'+dy'
\end{cases}
この連立方程式を $x',y'$ について解けば、関係を逆にして $x',y'$ を $x,y$ の一次式で表せます。
$y'$ の係数を揃えて消します。
\begin{cases}
dx=
adx'+bdy' \\
by=bcx'+bdy'
\end{cases}
\tag{2}
dx-by=(ad-bc)x'
$x'$ の係数を揃えて、消す際に $ad-bc$ が現れるように引きます。(理由は後述)
\begin{cases}
cx=acx'+bcy' \\
ay=acx'+ady'
\end{cases}
\tag{3}
ay-cx=(ad-bc)y'
解が得られました。
\tag{4}
\left\{\begin{aligned}
x'&=\frac{dx-by}{ad-bc} \\
y'&=\frac{-cx+ay}{ad-bc}
\end{aligned}\right.
$(1),(4)$ から右辺の係数を抜き出します。
\begin{pmatrix}a&b\\c&d\end{pmatrix},
\begin{pmatrix}
\frac{d}{ad-bc} & -\frac{b}{ad-bc} \\
-\frac{c}{ad-bc} & \frac{a}{ad-bc}
\end{pmatrix}
$(4)$ は $(1)$ の逆変換です。逆変換を行列の形にしたものは逆行列と呼びます。肩に $-1$ を付けることで逆行列を得る操作を表します。分数が並ぶと煩雑なため共通因子を括り出します。
逆行列
\begin{pmatrix}a&b\\c&d\end{pmatrix}^{-1}
=\frac{1}{ad-bc}
\begin{pmatrix}d&-b\\-c&a\end{pmatrix}
行列の成分を比較すると、対角線上(Xの字)のペアで、$a$ と $d$ は位置を入れ替えて、$b$ と $c$ は位置はそのままで符号を反転していることが分かります。
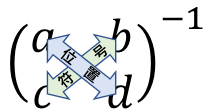
逆行列の成分は解を求める際の引き算に対応しています。これを示すために $(3)$ を $ay-cx$ としました。
\begin{array}{r}dx-by\\ay-cx=-cx+ay\end{array}
\ \mapsto\ \begin{pmatrix}d&-b\\-c&a\end{pmatrix}
実用上は $dx-by$ の対応を意識しておけば、$d$ が位置の入れ替えで、$-b$ が符号の反転だと分かるでしょう。$(2)$ を再掲します。分母の $ad-bc$ も現れます。
\tag{2}
dx-by=(ad-bc)x'
逆行列を持たない行列
逆行列には分数が現れるため、分母 $ad-bc=0$ のときに逆行列が求まりません。これは連立方程式が解けないことに対応します。
【例】
\begin{cases}
x=2x'+4y' \\
y=3x'+6y'
\end{cases}
2×6-4×3=0
右辺の係数を合わせて引くと $0$ になって解が求まりません。
\begin{cases}
3x=6x'+12y' \\
2y=6x'+12y'
\end{cases}
3x-2y=0
この関係を一般化すれば、右辺が定数倍の関係にあれば解が求まらず、$ad-bc=0$ となります。
\begin{cases}
x=ax'+by' \\
y=cx'+dy'=n(ax'+by')
\end{cases}
c=na,\ d=nb \\
ad-bc=a(nb)-b(na)=0
$b=ma$ とすれば、縦に定数倍の関係にあれば、横にも定数倍の関係にあることが分かります。特別な形として $n=0$ や $m=0$ の場合も含みます。また、行や列を入れ替えても同様です。
逆行列を持たない行列
\begin{pmatrix}a&b\\na&nb\end{pmatrix}
=\begin{pmatrix}a&ma\\c&mc\end{pmatrix}
=\begin{pmatrix}a&ma\\na&nma\end{pmatrix}
\begin{pmatrix}0&0\\0&0\end{pmatrix}
,\begin{pmatrix}a&b\\0&0\end{pmatrix}
,\begin{pmatrix}a&0\\c&0\end{pmatrix}
,\begin{pmatrix}0&0\\c&d\end{pmatrix}
,\begin{pmatrix}0&b\\0&d\end{pmatrix}
この節では逆行列を持つ、つまり $ad-bc≠0$ であるケースを考えます。
$(1),(4)$ を再掲します。
\tag{1}
\begin{cases}
x=ax'+by' \\
y=cx'+dy'
\end{cases}
\tag{4}
\left\{\begin{aligned}
x'&=\frac{dx-by}{ad-bc} \\
y'&=\frac{-cx+ay}{ad-bc}
\end{aligned}\right.
$(1)$ に $(4)$ を代入すれば元に戻ります。
\tag{1'}
\left\{\begin{aligned}
x&=a\left(\frac{ dx-by}{ad-bc}\right)
+b\left(\frac{-cx+ay}{ad-bc}\right)
=\frac{
adx-bcx}{ad-bc}=x \\
y&=c\left(\frac{ dx-by}{ad-bc}\right)
+d\left(\frac{-cx+ay}{ad-bc}\right)
=\frac{ady-bcy}{ad-bc}=y
\end{aligned}\right.
$(4)$ に $(1)$ を代入しても元に戻ります。
\tag{4'}
\left\{\begin{aligned}
x'&=\frac{d(ax'+by')-b(cx'+dy')}{ad-bc}
=\frac{
adx'-bcx'}{ad-bc}=x' \\
y'&=\frac{-c(ax'+by')+a(cx'+dy')}{ad-bc}
=\frac{ady'-bcy'}{ad-bc}=y'
\end{aligned}\right.
$(1')$ と $(4')$ を行列の積で表せば、行列と逆行列の積、逆行列と行列の積が単位行列になることに対応します。
逆行列の性質
\begin{pmatrix}a&b\\c&d\end{pmatrix}
\begin{pmatrix}a&b\\c&d\end{pmatrix}^{-1}
=\begin{pmatrix}a&b\\c&d\end{pmatrix}^{-1}
\begin{pmatrix}a&b\\c&d\end{pmatrix}
=I
このように逆行列が存在すれば変換結果を元に戻せます。
逆行列を持つ行列を正則であると表現して、正則行列と呼びます。
正則行列
行列 $\begin{pmatrix}a&b\\c&d\end{pmatrix}$ は $ad-bc≠0$ のときに正則(
逆行列を持つ)
変換が一方通行でないのは重要な性質です。そのため特別な名前が付いています。
◀前の記事 ▲記事一覧 次の記事▶
